Cara Mencari Sisi Miring Trapesium, Pahami Rumus dan Pembahasannya

Trapesium secara umum dapat didefinisikan sebagai berikut. Trapesium adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang dua di antaranya saling sejajar namun tidak sama panjang. Secara sederhana trapesium juga dapat dijelaskan sebagai berikut, trapesium adalah segi empat yang mempunyai sepasang sisi yang tepat berhadapan dan sejajar.

Jenis-Jenis Trapesium
Terdapat beberapa jenis bangun datar trapesium. Berikut ini adalah penjelasannya.

- Trapesium Sembarang
Trapesium sembarang dapat dijelaskan sebagai berikut, trapesium sembarang memiliki panjang kaki yang tidak sama, kaki-kakinya juga tidak seimbang atau tidak sama ke arah sisi sejajarnya. Trapesium sembarang adalah trapesium yang keempat rusuknya tidak sama panjang.

- Trapesium Siku-Siku
Trapesium siku-siku memiliki sudut yang kakinya tegak lurus pada sisi sejajarnya. Trapesium ini memiliki sudut siku-siku di salah satu sisinya, sementara sisi lainya tetap membentuk sudut lancip dan tumpul.

- Trapesium Sama Kaki
Trapesium sama kaki ini mempunyai sepasang rusuk sama panjang dan sepasang rusuk sejajar. Trapesium sama kaki mempunyai satu simetri lipat.

Sifat Trapesium
Selain dari jenis-jenisnya, perlu mengetahui juga sifat-sifat dari trapesium. Sama halnya bangun datar yang lainya, trapesium juga memiliki sifat-sifatnya tersendiri. Berikut ini adalah sifat-sifat trapesium, simak lebih lanjut. Dan dari uraian di atas diperoleh sifat-sifat trapesium:

- memiliki sepasang sisi sejajar
- jumlah dua sudut berdekatan (sudut dalam sepihak) adalah 180 derajat
- trapesium siku-siku, salah satu kakinya tegak lurus terhadap sisi sejajarnya

Rumus Sisi Miring Trapesium
Untuk mencari panjang sisi miring suatu trapesium, dapat menggunakan rumus kuadrat sisi miring trapesium dapat dicari dengan cara menjumlahkan kuadrat tinggi trapesium dengan kuadrat alas trapesium (setelah terlebih dahulu dikurangi dengan sisi atas trapesium).

Penjelasan lebih detil, dapat disimak pada pembahasan berikut:

Pencarian sisi miring pada trapesium dapat mencarinya terlebih dahulu menggunakan rumus Teorema Pythagoras yang menyatakan bahwa jumlah kuadrat dua sisi segitiga siku-siku, akan sama dengan kuadrat sisi miring (hipotenusa) segitiga siku-siku tersebut.

Teorema ini biasa digunakan untuk menentukan panjang sebuah sisi pada segitiga siku-siku jika panjang dua sisi yang lain diketahui. Di mana sisi miring pada trapesium umumnya berbentuk atau membentuk segitiga. Secara umum, pada segitiga siku-siku berlaku aturan berikut:

c²= a² + b²

di mana:
c = panjang sisi miring
a dan b = panjang sisi siku-siku

Contoh Soal
1. Dari gambar tersebut diketahui: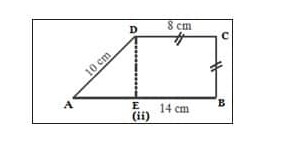

BC = CD = 8 cm
AD = 10 cm
EB = 14 cm
Untuk mencari luas bangun trapesium (ii) terlebih dahulu harus mencari panjang AE. Untuk mencari panjang AE bisa menggunakan rumus teorema Pythagoras, yaitu:

AE = √(AD2 – CD2)
= √(102 – 82)
= √(100 – 64)
= √36
= 6 cm

Setelah didapat panjang AE, maka panjang AB:
AB = AE + EB
= 6 cm + 14 cm = 20 cm

Untuk mencari luas trapseium (ii) kita gunakan rumus luas trapesium yaitu:
Luas = ½ x (CD + AB) x t
= ½ x (8 cm + 20 cm) x 8 cm
= 112 cm2


2. Dari gambar tersebut diketahui: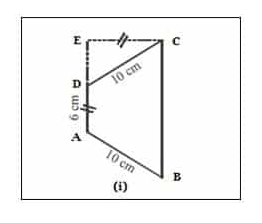

AD = CE = 6 cm
AB = CD = 10 cm
Untuk  mencari  luas  bangun trapesium (i)  terlebih  dahulu  harus  mencari panjang  BC,  panjang  BC  akan  didapat  jika  panjang  DE  diketahui.  Untuk mencari panjang DE gunakan rumus teorema Pythagoras, yaitu:

DE = √(CD2 – CE2)
DE = √(102 – 62)
DE = √(100 – 36)
DE = √64 = 8 cm

Karena bangun trapesium (i) merupakan trapesium sama kaki, maka:
BC = AD + 2 x DE
BC = AD + 2 x DE
= 6 cm + 2 x 8 cm
= 22 cm

Untuk mencari luas trapseium (i) kita gunakan rumus luas trapesium yaitu:

Luas = ½ x (AD + BC) x t
= ½ x (6 cm + 22 cm) x 8 cm
= 112 cm2

3. Untuk lebih jauh memahami dari sisi trapesium ini, silahkan perhatikan gambar trapesium berikut: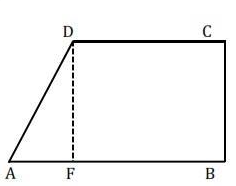

Sisi miring trapesium adalah AD
AF = AB - CD
FD = BC

Gunakan segitiga AFD untuk mencari panjang sisi miring trapesium tersebut.

AD²= AF² + FD²

AD = sisi miring
AF = sisi alas trapesium dikurangi dengan sisi atas trapesium
FD = tinggi trapesium

Jadi, kuadrat sisi miring trapesium dapat dicari dengan cara menjumlahkan kuadrat tinggi trapesium dengan kuadrat alas trapesium (setelah terlebih dahulu dikurangi dengan sisi atas trapesium).